Основания трапеции равны \(\displaystyle 8\) и \(\displaystyle 34\small, \) площадь равна \(\displaystyle 168\small. \) Найдите её высоту.
Воспользуемся одной из формул для вычисления площади трапеции.
Формула площади трапеции
\(\displaystyle S=\frac{a+b}{2} \cdot h \small,\)
где \(\displaystyle a\) и \(\displaystyle b\) – основания трапеции,
\(\displaystyle h\) – высота трапеции.
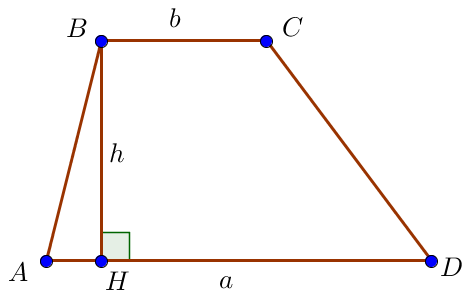
Поскольку \(\displaystyle \color{blue}{a}=\color{blue}{34} \small,\) \(\displaystyle \color{magenta}{b}=\color{magenta}{8}\) и \(\displaystyle \color{green}{S_{трап}}=\color{green}{168}{\small,}\) то
\(\displaystyle \color{green}{168} = \frac{\color{blue}{34}+\color{magenta}{8}}{2}\cdot h {\small,}\)
откуда
\(\displaystyle {168} = 21\cdot h \;\;\; | : \color{red}{21}{\small,}\)
\(\displaystyle h={8}{\small . }\)
Ответ: \(\displaystyle 8{\small .}\)
