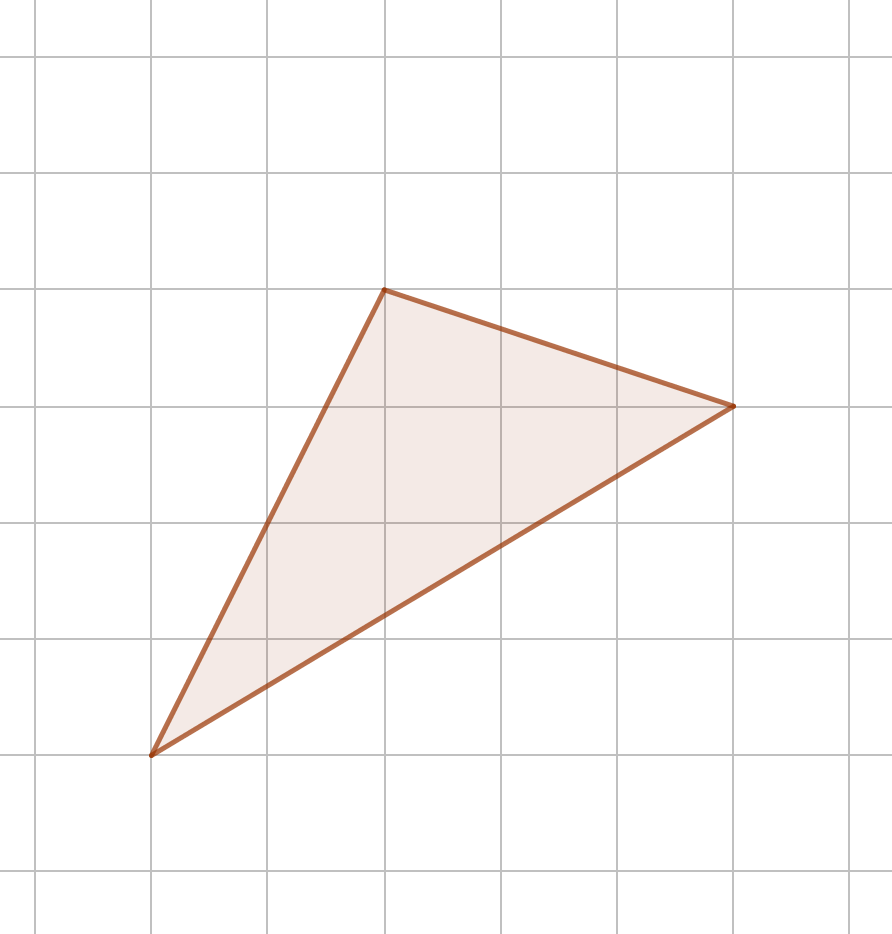
Достроим данный треугольник прямоугольными треугольниками так, чтобы получилась фигура с легко вычисляемой площадью.
 

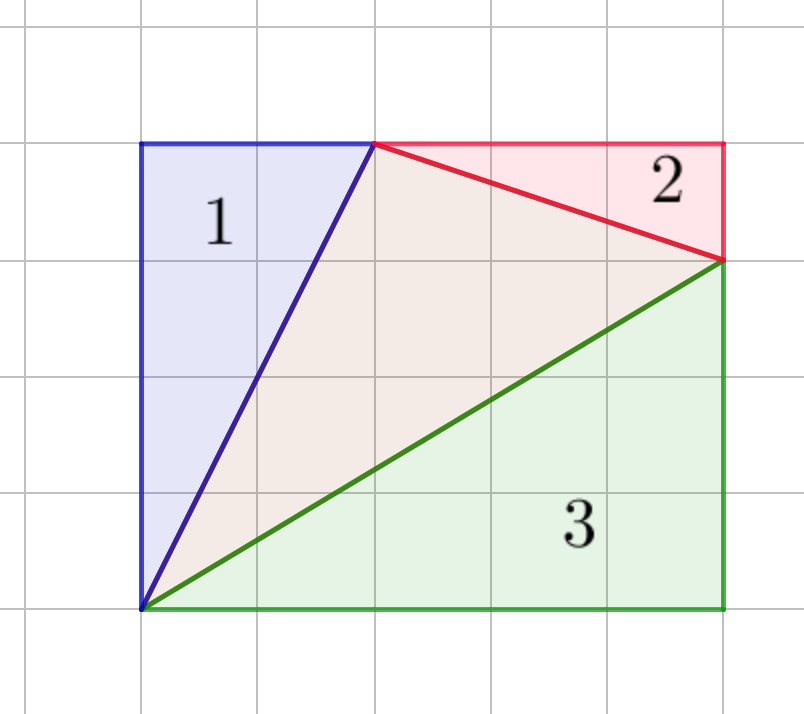
Получили прямоугольник со сторонами \(\displaystyle 4\) и \(\displaystyle 5{\small . }\) Площадь искомого треугольника равна площади полученного прямоугольника без площадей достроенных прямоугольных треугольников.

Площадь прямоугольника равна

\(\displaystyle 4 \cdot 5=20{\small , }\)

площадь первого треугольника равна

\(\displaystyle \frac{1}{2}\cdot 4 \cdot 2=4{\small , }\)

площадь второго треугольника равна

\(\displaystyle \frac{1}{2}\cdot 3 \cdot 1=\frac{3}{2}{\small , }\)

площадь третьего треугольника равна

\(\displaystyle \frac{1}{2}\cdot 3 \cdot 5=\frac{15}{2}{\small . }\)

Таким образом, площадь искомого треугольника равна

\(\displaystyle 20-4-\frac{3}{2}-\frac{15}{2}=7{\small . }\)

Ответ: \(\displaystyle 7{\small . }\)