Задание
Выберите график квадратичной функции \(\displaystyle y=-\frac{1}{4}x^2{\small :}\)
| \(\displaystyle 1\) | 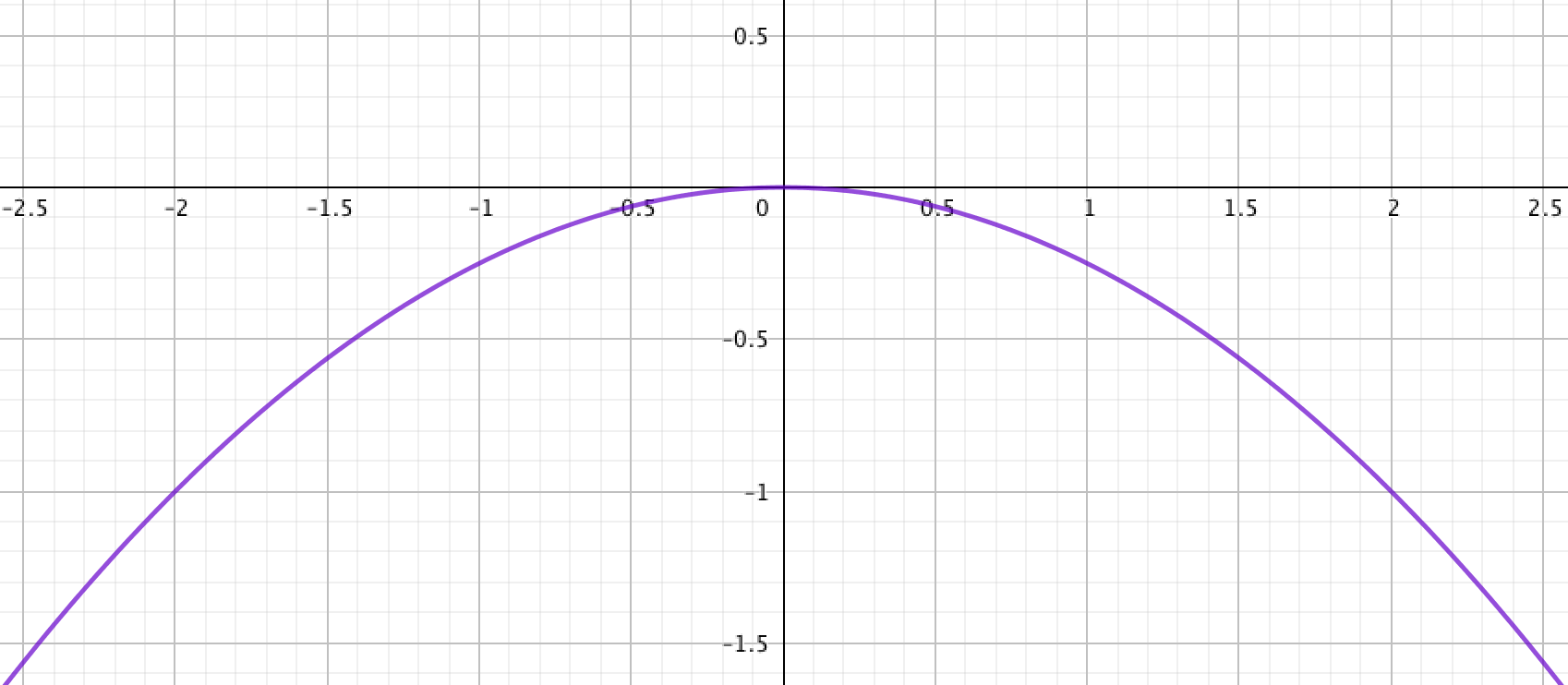 | \(\displaystyle 2\) | 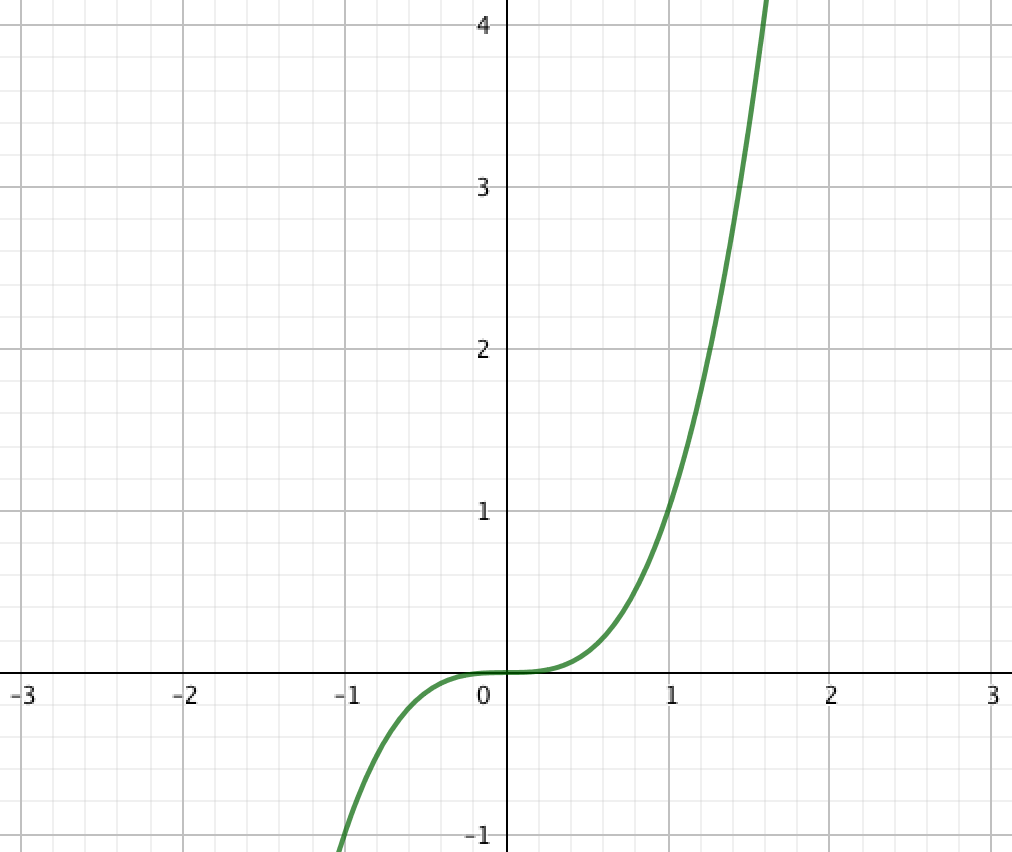 |
| \(\displaystyle 3\) | 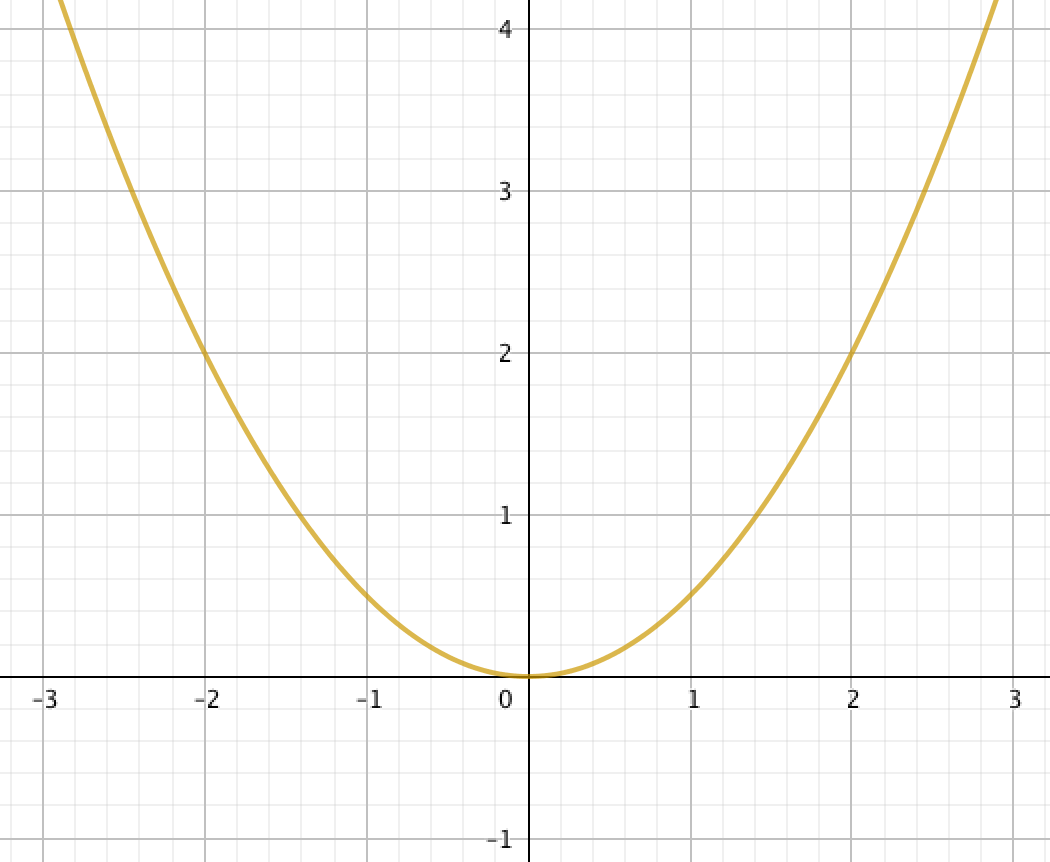 | \(\displaystyle 4\) | 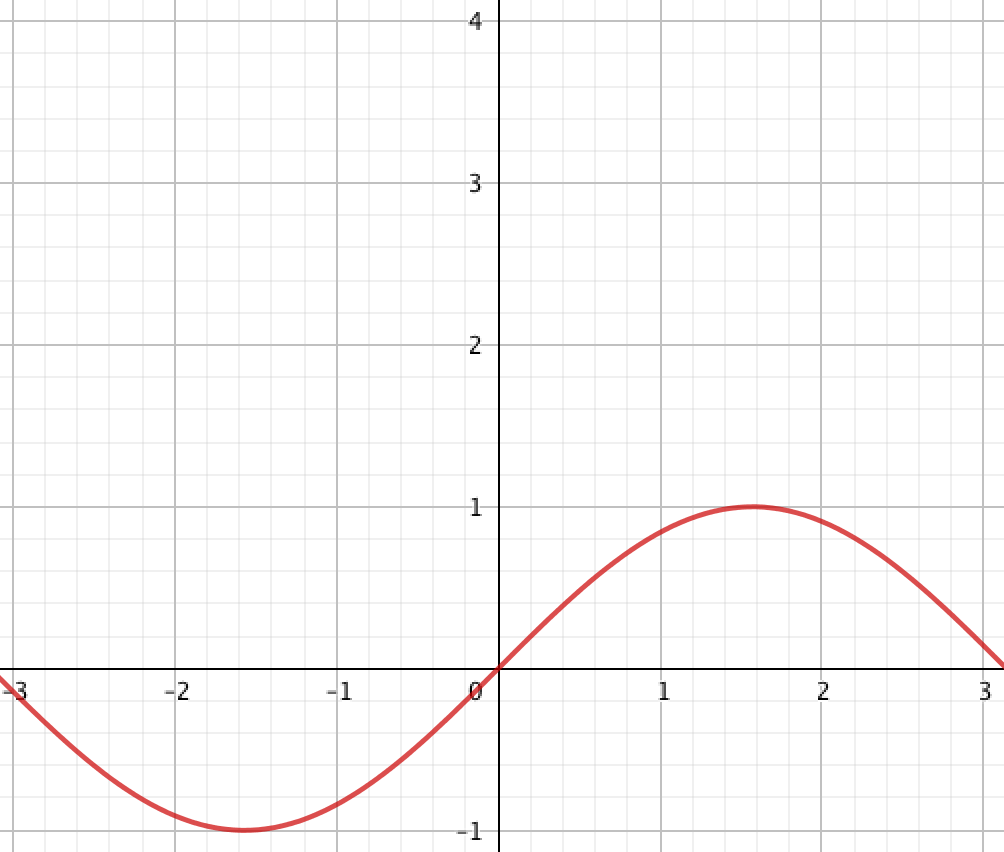 |
Решение
Построим график квадратичной функции \(\displaystyle y=-\frac{1}{4}x^2\) по точкам. Для этого составим таблицу значений:
| \(\displaystyle x\) | \(\displaystyle -2{,}5\) | \(\displaystyle -2\) | \(\displaystyle -1{,}5\) | \(\displaystyle -1\) | \(\displaystyle -0{,}5\) | \(\displaystyle 0\) |
| \(\displaystyle y=-\frac{1}{4}x^2\) | \(\displaystyle -1{,}5625\) | \(\displaystyle -1\) | \(\displaystyle -0{,}5625\) | \(\displaystyle -0{,}25\) | \(\displaystyle -0{,}0625\) | \(\displaystyle 0\) |
| \(\displaystyle x\) | \(\displaystyle 0{,}5\) | \(\displaystyle 1\) | \(\displaystyle 1{,}5\) | \(\displaystyle 2\) | \(\displaystyle 2{,}5\) |
| \(\displaystyle y=-\frac{1}{4}x^2\) | \(\displaystyle -0{,}0625\) | \(\displaystyle -0{,}25\) | \(\displaystyle -0{,}5625\) | \(\displaystyle -1\) | \(\displaystyle -1{,}5625\) |
Обозначим данные точки на плоскости:
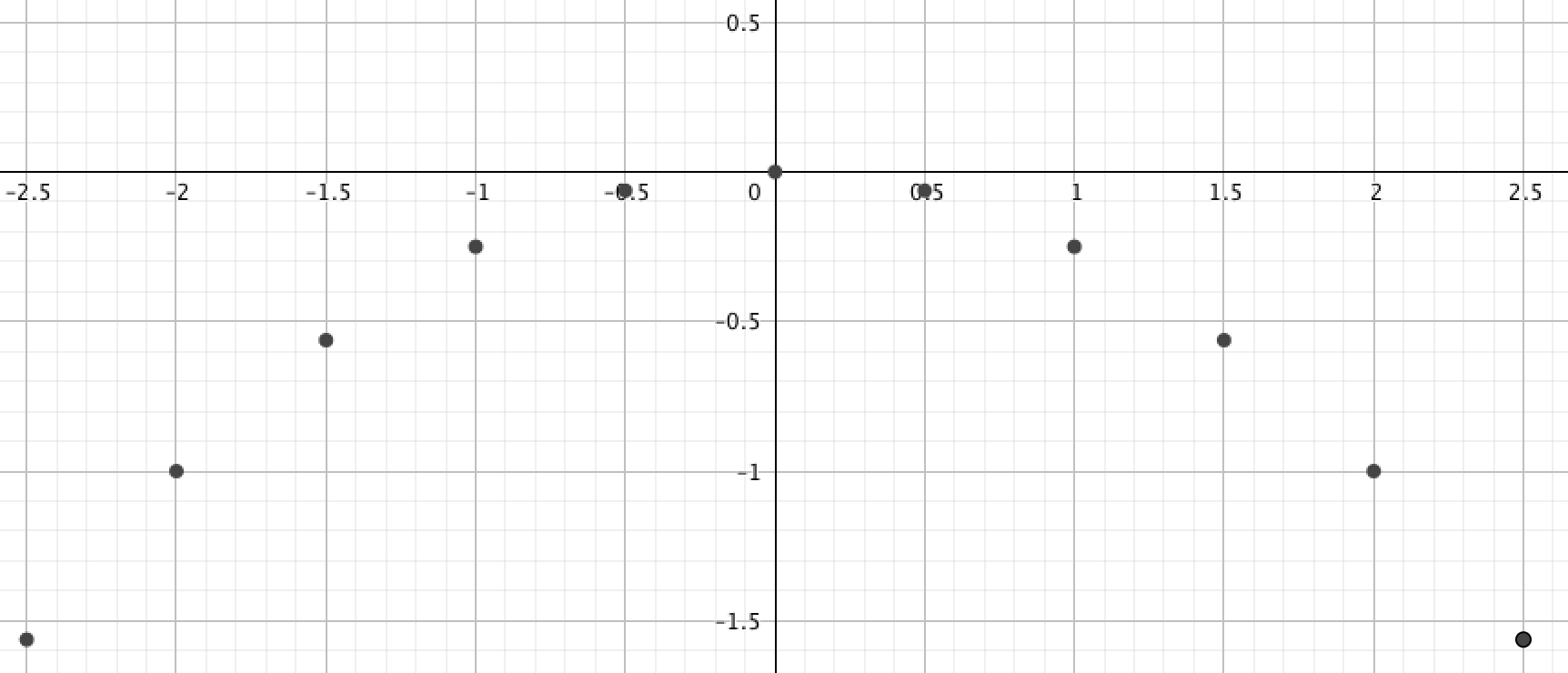
и соединим их:
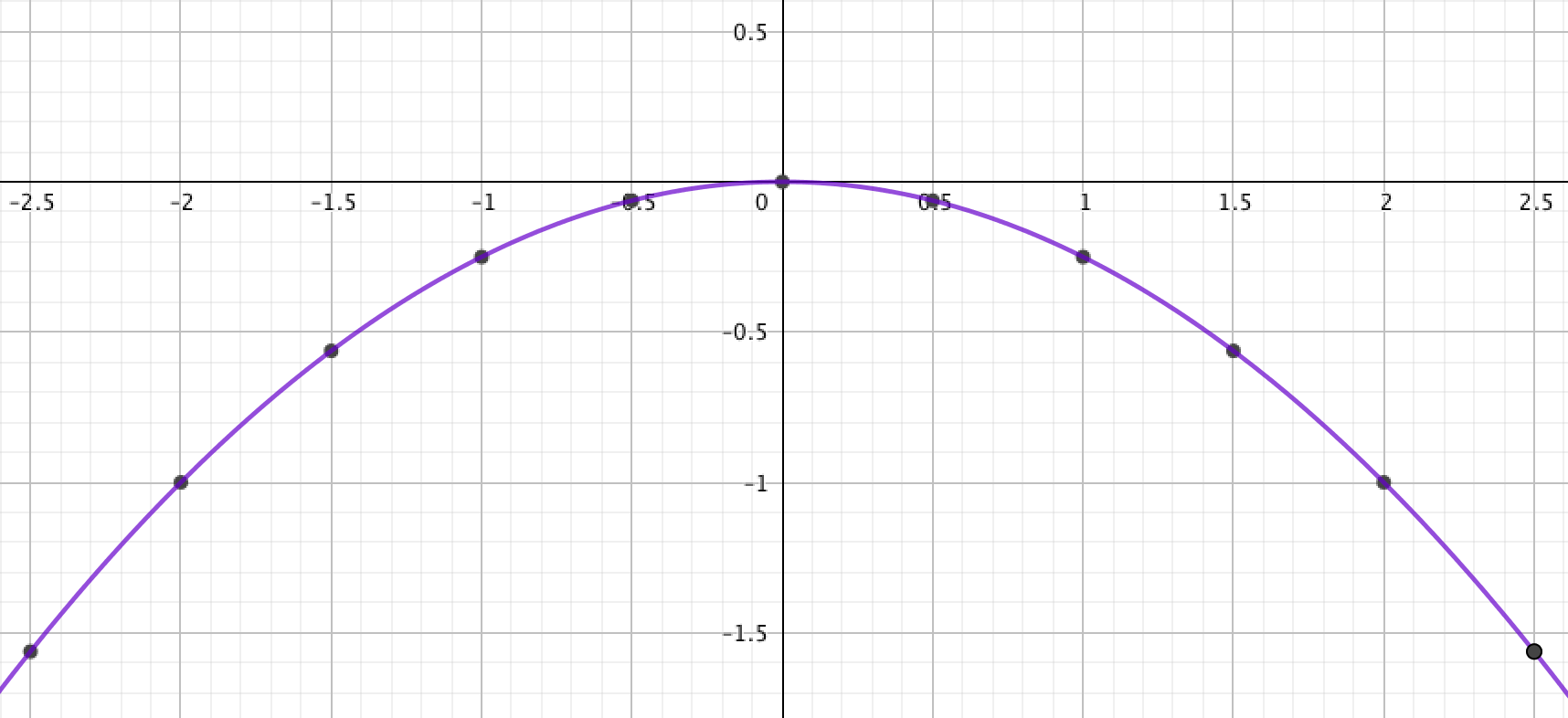
Сравнивая с полученным графиком квадратичной функции \(\displaystyle y=-\frac{1}{4}x^2\) данные в задаче графики,
| \(\displaystyle 1\) |  | \(\displaystyle 2\) |  |
| \(\displaystyle 3\) |  | \(\displaystyle 4\) |  |
получаем, что графику квадратичной функции \(\displaystyle y=-\frac{1}{4}x^2\) соответствует вариант \(\displaystyle 1{\small .}\)
Ответ: \(\displaystyle 1{\small .}\)
