Задание
Фигура нарисована на сетке из единичных квадратов. Найдите длину дуги закрашенного сектора.
\(\displaystyle l=\)
\(\displaystyle \pi\)
Решение
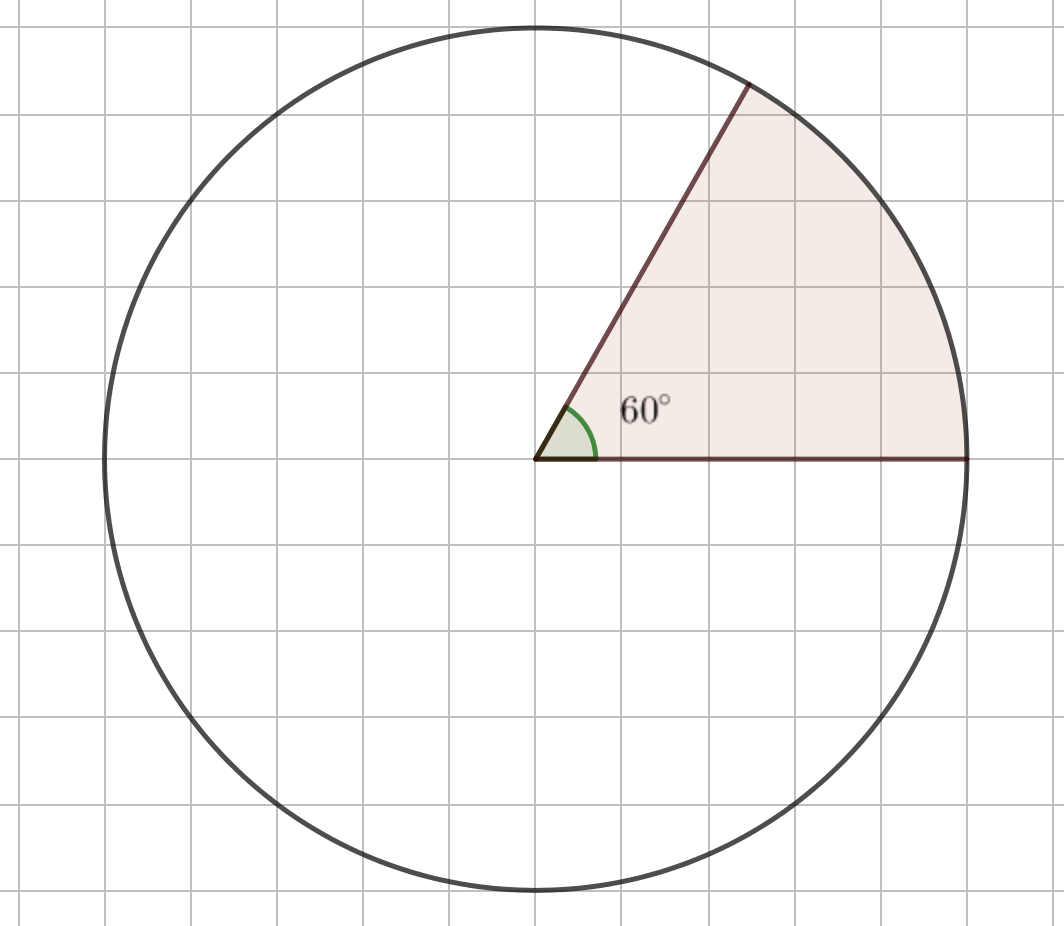
Из рисунка видно, что радиус окружности равен \(\displaystyle 5{\small : }\)
Воспользуемся формулой.
Правило
Длина дуги
Длина дуги окружности радиуса \(\displaystyle R{\small , }\) заключенной между сторонами угла в \(\displaystyle \alpha \) градусов, равна
\(\displaystyle \frac{\pi \cdot \alpha \cdot R}{180}{\small .}\)
Таким образом, искомая длина дуги окружности радиуса \(\displaystyle 5{\small , }\) заключенной между сторонами угла в \(\displaystyle 60\) градусов, равна
\(\displaystyle \frac{\pi\cdot 60\cdot 5}{180}=\frac{5}{3}\pi{\small .}\)
Ответ: \(\displaystyle \frac{5}{3}\pi{\small .}\)