Найдите площадь \(\displaystyle S\) большого круга без учета площади внутреннего круга, если нанесена сетка с единичными квадратами. В ответ запишите \(\displaystyle \frac{S}{\pi}\small. \)
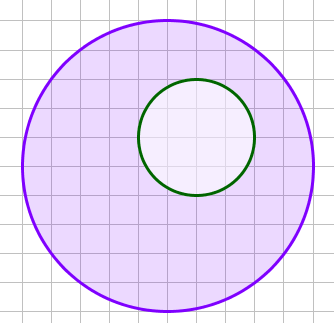
Радиус внутреннего круга равен \(\displaystyle r=2 \small. \) Площадь внутреннего круга равна \(\displaystyle S_1=\pi \cdot r^2=\pi \cdot 2^2=4 \pi \small. \\ \) Радиус большого круга равен \(\displaystyle R=5 \small. \) Площадь большого круга равна \(\displaystyle S_2=\pi \cdot R^2=\pi \cdot 5^2=25 \pi \small.\\ \) | 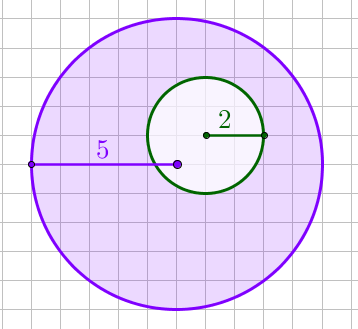 |
Площадь искомой области равна разности площадей большого и внутреннего кругов:
\(\displaystyle S=S_2-S_1=25\pi-4\pi=21\pi{\small .}\)
Тогда
\(\displaystyle \frac{S}{\pi}=\frac{21\pi}{\pi}=21 \small. \)
Ответ: \(\displaystyle 21 {\small .}\)
