Сначала найдем высоту равностороннего треугольника со стороной \(\displaystyle a\small,\) а затем найдем радиус описанной окружности.
Проведем высоту \(\displaystyle BH\) равностороннего треугольника \(\displaystyle ABC \small.\)
Так как высота \(\displaystyle BH\) равностороннего треугольника является и его медианой, то
\(\displaystyle AH=\frac{1}{2} \cdot AC=\frac{a}{2} \small.\)
Найдем длину отрезка \(\displaystyle BH\) из прямоугольного треугольника \(\displaystyle ABH \small.\)
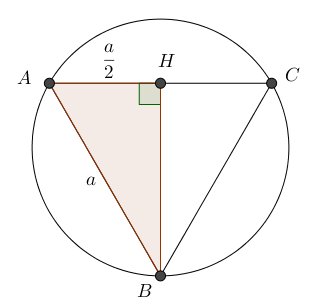 | По теореме Пифагора \(\displaystyle AB^2=AH^2+BH^2 \small.\) Тогда \(\displaystyle BH^2=AB^2-AH^2 \small,\) \(\displaystyle BH^2=a^2-\left( \frac{a}{2}\right)^2=a^2-\frac{a^2}{4}=\frac{3a^2}{4}\small.\) Поскольку длина отрезка положительна, то \(\displaystyle BH=\frac{a\sqrt{3}}{2} \small.\) |
Пусть точка \(\displaystyle O\) – центр описанной окружности. Центр описанной около треугольника окружности – точка пересечения серединных перпендикуляров.
Серединные перпендикуляры равностороннего треугольника являются также высотами. Значит, точка \(\displaystyle O\) лежит на высоте \(\displaystyle BH \small.\)
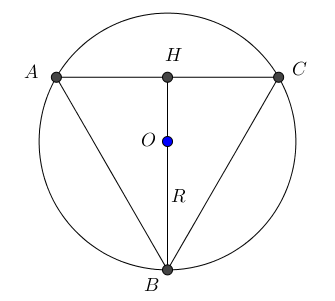
Высота равностороннего треугольника является также медианой. Значит, \(\displaystyle O\) – точка пересечения медиан.
Тогда точка \(\displaystyle O\) делит медиану \(\displaystyle BH\) в отношении \(\displaystyle 2:1\small,\) считая от вершины \(\displaystyle B \small.\)
Следовательно,
\(\displaystyle R=OB=\frac{2}{3} \cdot BH=\frac{2}{3} \cdot \frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3} \small.\)
